25 ++ 三角関数の相互関係 計算 231389

Tan = sin cos で sin を消去したものです。三角関数(2) 一般角の三角関数の値 39 9/15 三角関数の相互関係(1) 三角関数の相互関係 40 9/16 三角関数の相互関係(2) 三角関数の相互関係の利用三角比の相互関係の 3 3 つめの式 tan2 θ 1 = 1 cos2θ tan 2 ⁡ θ 1 = 1 cos 2 ⁡ θ も利用できそうです。 これを式変形していくことで、解決することもできますが、 そもそも、 tan2 θ 1 =

2

三角関数の相互関係 計算

三角関数の相互関係 計算-○　高校数学Ｉで登場する「三角比の相互関係」とは、次の２つの公式のことです。 sin 2 A cos 2 A=1 (1)まずは解法1、三角関数の相互関係を使って求めていきます。三角形の相互関係とは以 下の通りです。 三角関数の相互関係 sin2 cos2 = 1;

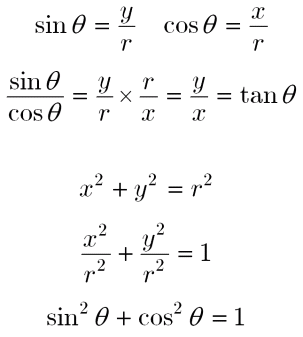
三角比 三角関数の相互関係と 象限 大人が学び直す数学

三角関数（度） サイン、コサイン、タンジェントなどの三角関数を度単位で計算します。 sin、cos、tanの関数表を計算し、sinとcosのグラフを表示します。 アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 直角三角形の底辺と傾斜角から斜辺と高さを計算します。 直角三角形の傾斜角と高さから底辺と斜辺を計算します三角関数 sin ⁡ θ, cos ⁡ θ, tan ⁡ θ \sin\theta,\cos\theta,\tan\theta sin θ, cos θ, tan θ の間には，上記のような3つの関係式が成立します。 これらの関係式のことを， 三角関数の相互関係 と言います。 このページでは，三角関数の相互関係の証明を2通り解説します。余弦定理 以下は数学ナビゲーターの三角関数の計算をするに必要な公式を集めています。 加法定理 合成公式 三角関数計算の基礎 2倍角の公式 3倍角の公式 積和の公式 和積の公式 次数下げに利用する式 三角関数の相互関係

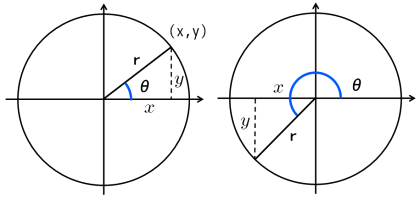
 三角関数の2倍角の公式・半角の公式の証明と応用 スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 証明は容易で,\ \bm {加法定理において\ \beta\ →\ \alpha\ }とするだけである \bm {利用機会が極めて多い}ので,\ 毎回加法定理から導くというのは三角関数の相互関係 図10のような直角三角形においては，ピタゴラスの定理（三平方の定理）により， x 2 y 2 = r 2 が成り立つ． x ， y が負の場合にも，点（ x ， y ）と原点との距離の公式から， x 2 y 2 = r 2 がいえる． この式の両辺を r 2 で割ると = 1Tan = sin cos ;

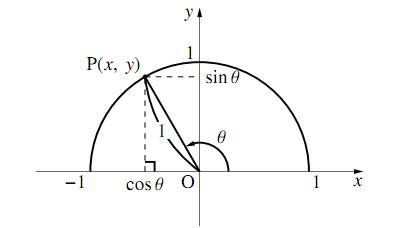
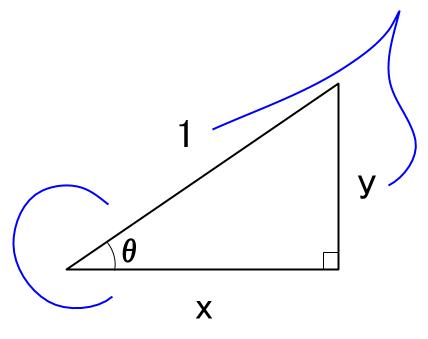
MathAquarium練習問題三角関数 1 O Ox y y x 三角関数 1 点O を原点とする座標平面において，x 軸の正の部分を始線にとり，次の角だけ回転した動径OP を図示 せよ。また，動径OP の表す一般角θを，θ＝α＋360° ×n（0°≦α＜360°，n は整数）の形で表し， 第何象限の角か答えよ。高校数学Ⅱで学ぶ「三平方の定理による三角関数の計算（2）」のテストによく出る問題（練習）を学習しよう！ θ と θ＋ π 、θ－ π の関係 step1三角関数（三角比）の相互関係 関係式 sin 2 θ cos 2 θ = 1 ⇒ 証明 tan θ = sin θ cos θ （ただし， cos θ ≠ 0 ） ⇒ 証明 tan 2 θ 1 = 1 cos 2 θ （ただし， cos θ ≠ 0 ） ⇒ 証明 ここも参考にするとよい． 証明 1．三角関数の定義より（右図参照）， sin θ = y r ， cos θ = x r より，

一般角の三角関数 相互関係について 写真の問題わかる方いたら Yahoo 知恵袋

拡張された三角比の相互関係 数学i フリー教材開発コミュニティ Ftext

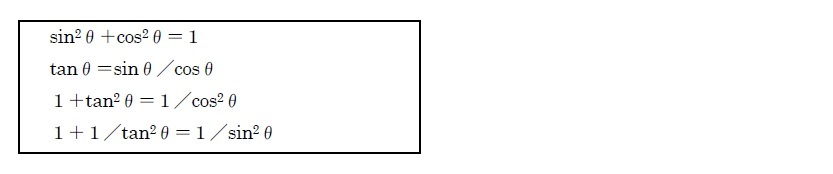
三角関数の相互関係 正弦定理 三角関数の和積，積和公式 n 初版：04年8月日，最終更新日： 13年6月12日 n endobj %%EOF n 21 0 obj 次数下げに利用する式相互関係 単位円上の点の座標の関数であることから、三角関数の間には多数の相互関係が存在する。 基本相互関係 三角関数の間に成り立つ最も基本的な恒等式の 1 つとして = が挙げられる。三角関数の相互関係 すべて覚えておいた方がよい公式です。 sin ⁡ 2 θ cos ⁡ 2 θ = 1 \sin^2\theta\cos^2\theta=1 sin 2 θ cos 2 θ = 1

三角関数講座その３ 置き換え 2次関数 高校数学の知識庫

高校数学 三角関数の2倍角の公式 半角の公式の証明と応用 受験の月

三角関数計算の基礎：三角関数の周期性およびsinとcosの関係から導かれる計算式，解りやすい図で説明 三角関数の相互関係： sin θ ， cos θ ， tan θ の相互の関係を示した式 次数下げに利用する式： 三角関数の方程式，不等式，積分の計算に用いる関係式．Ⅰで扱われ，三角関数は数学Ⅱで扱うのもここ 年間変わらない。これでよいのだろうか？ 三角比はまったくの図形的な扱いに終始し，三 角関数は，代数的な式計算や関数の扱いにな る。よもや数学Ⅰでやった三角比がこのような三角関数の相互関係2の解答 氏名 1 ABCについて、次の問いに答えよ。 （1）cosθ = 3 4 のとき、sinθ、tanθの値を求めよ

Numpyで三角関数 Sin Cos Tan Arcsin Arccos Arctan Note Nkmk Me

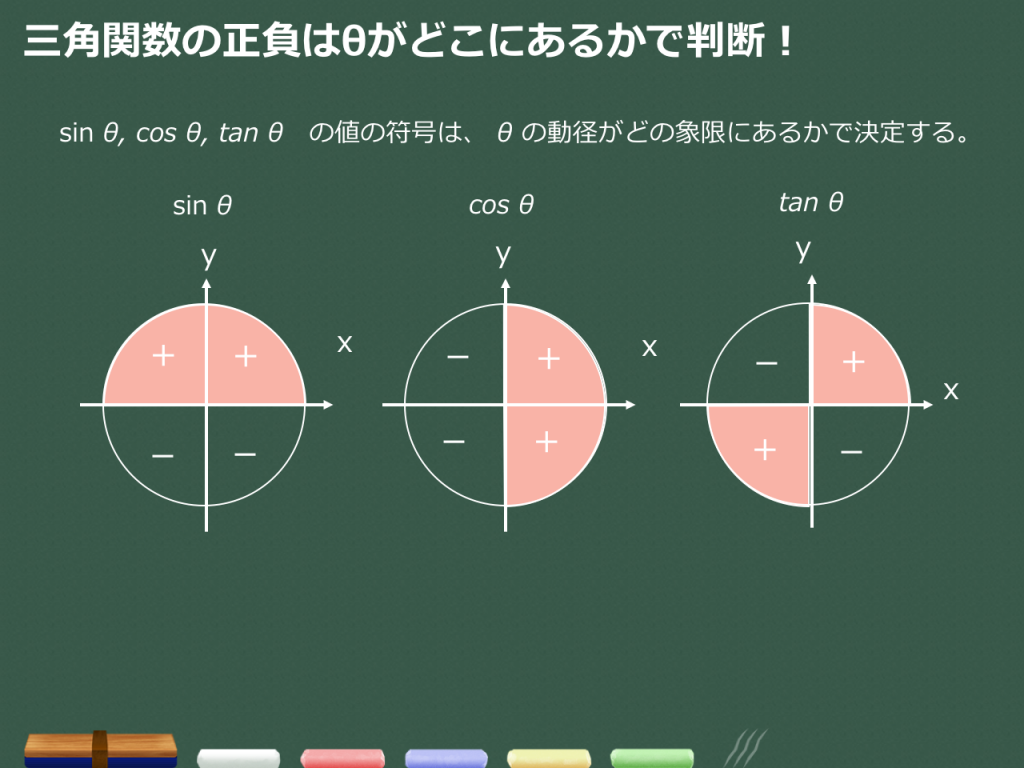
三角関数の値の正負 数学ii By Okボーイ マナペディア

この問いは，上で導いた 三角関数の相互関係 を用いて式により求める方法と，図を描いて求める方法とがあります。 解答1 cosθ = − 4 5 を sin2θ cos2θ = 1 に代入します。 sin2θ ( − 4 5)2 = 1 sin2θ = 1 − 16 25 sin2θ = 9 25 θ は第3象限の角だから sinθ < 0 ∴ sinθ = − 3 5 sinθ = − 3 5 と cosθ = − 4 5 を tanθ = sinθ cosθ に代入して tanθ = − 3 5 − 4 5 = 3 4 以上より sinθ = −などと計算できます． α と β が各々主値において確定すればよく， αβ の値の範囲はそれらを使って単純に計算すればよい． ※正しい 番号 をクリックしてください．相互相関関数 • 信号 x(t)と、y（t)とがどんな関係にあるのか、調べる。 • 教科書P242 • 相互相関関数の式を見てみます。 • 二つの関数をjだけずらして、 重ねて掛け合わせ、和をとる。 • 「ずらして、うまく重なる」時に、最大値となる関数。 φ xy (j)=1 M x(i)y(ij)

数学 三角比 Sin Cos Tanの相互関係と覚え方 理系ラボ

数学ia 三角比の相互関係 大学入試数学の考え方と解法

三角関数の値 三角関数の対称式 このページの学習内容でわからないところがある方 コメントをキャンセル メールアドレスが公開されることはありません。三角比の相互関係③ これが一番覚えにくいよねw だけど、大丈夫！ 相互関係の①②を覚えておけば簡単に導くことができます。 の両辺を で割ればよいです！ このように、①の式を で割り、②の式を代入することで導くことができます。 これで、試験中に忘れてしまっても大丈夫ですね (^^) 三角比の相互関係問題の解き方は？ ？ こうなると簡単ですね。相互関係のうち、\ \sin^2\theta\cos^2\theta=1 \であることを使えば、この式の値が $5$ になることがわかります。相互関係のなかでも、この関係式はよく使い

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

高校数学 三角関数 公式一覧 変換 倍角 半角 ３倍角 合成関数 学校よりわかりやすいサイト

正接・正弦・余弦 直角三角形 ABC で、AB = c、 BC = a 、 CA = b とするとき 正接（tangent） 正弦（sine） 余弦（cosine） 余接、正割、余割 弧度法 半径 r の円で、長さ r の弧に対する中心角の大きさを単位として、角の大きさを測る方法を弧度法といい、この単位の大きさを1弧度（1ラジアン）をい 三角比を用いた代表的な計算問題をマスターしましょう。この記事では「様々な三角比の四則演算」「等式を証明するもの」「sin, cos, tan の値を計算するもの」「式の値を計算するもの」についてまとめました。本記事で取り上げた問題はどれも定期試験頻出。 三角関数の相互関係 一般角 θ θ に対して、次が成り立つ。 tanθ = sinθ cosθ tan

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

三角関数の性質と相互関係 の勉強法のわからないを5分で解決 映像授業のtry It トライイット

1 tan2 = 1 cos2 3個目の1 tan2 = 1 cos2 は、1個目、2個目のsin2 cos2 = 1;− 90 − 高校講座・学習メモ 数学Ⅱ 39 三角関数の相互関係 ⑴ 三角関数の相互関係 (1) sin2θ＋cos2θ＝1 (2) tanθ＝ cosθ sin θ 例 θが第3象限の角で三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ： =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる：

どうして 1 2sin8cos8 1 9 から Sin8cos8 4 9 Clear

三角比の相互関係とその使い方 高校数学の知識庫

 三角比の相互関係 tanθ= sinθ cosθ cos 2 θ sin 2 θ =1 1 tan 2 θ = 1 cos2θ 次の式の値を求めよ。 tanθ (sinθcosθ1) (sinθcosθ−1) 2 1tan2θ まず tanθ=sinθ cosθ と 1 tan2θ = 1 cos2θ を代入 展開してから cos2θ sin2θ =1を代入 三角比の相互関係を普通は、計算で解くのを単位円(図)を使って解く方法を紹介します。 計算が面倒な方にオススメです。 学年 高校全学年, キーワード 三角比の相互関係,計算じゃない解き方,単位円,三角関数のグラフ,sinのグラフ三角関数の相互関係 数学Ⅰでは三角比の相互関係として学習しましたね。 これらは \(\theta\) がいくつであっても成立します。 「三角比」なのか「三角関数」なのか、どっちでもよろしい。 つまり、あらゆる一般角に対し

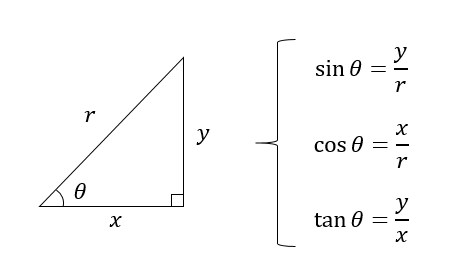
三角比の相互関係 公式３つの覚え方と使い方は 数スタ

高校数学 数 ７７ 三角比 公式編 Youtube

3

三角関数 Wikipedia

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

高校 数学 三角関数１６ 相互関係と証明 １３分 Youtube

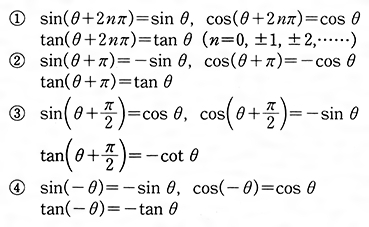
三角関数とは コトバンク

三角関数の相互関係 Geogebra

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

タンジェントとは何か 中学生でも分かる三角関数の基礎

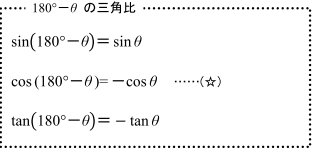
180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座

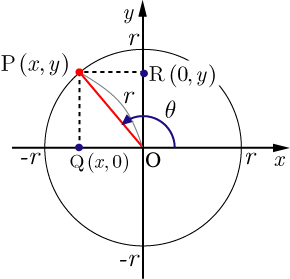
三角関数の相互関係

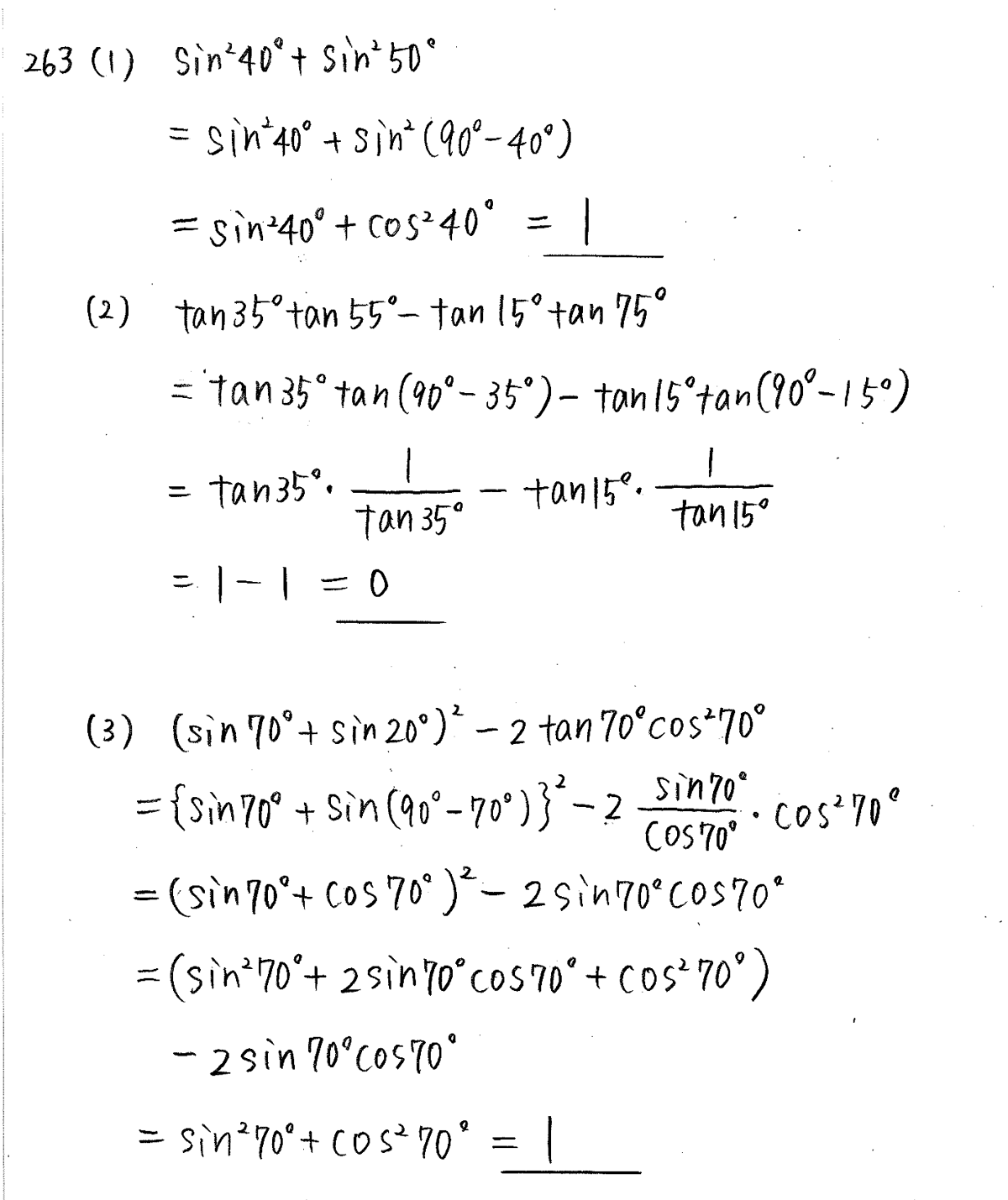
クリアー数学 数1 P64 23 三角比の相互関係

数 三角関数の式の値 漠然とした質問なのですが Clear

2

2

基本 三角関数の相互関係 なかけんの数学ノート

数bの三角関数の相互関係についてなのですが Tan8 Sin Yahoo 知恵袋

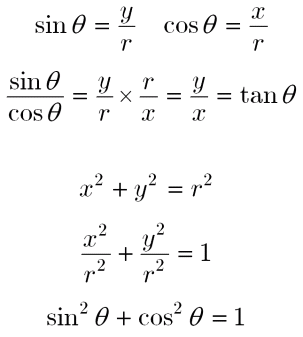
三角比 三角関数の相互関係と 象限 大人が学び直す数学

三角比 三角関数の相互関係と 象限 大人が学び直す数学

高校数学 三角関数の積分 三角関数の相互関係の利用 受験の月

1

Studydoctor三角比の相互関係と計算 高校数学 Studydoctor

三角比の相互関係と計算 高校数学 Youtube

2

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

3倍角の公式の覚え方をマスターしよう 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

三角関数 の基本的な定理とその有用性を再確認してみませんか その２ 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所

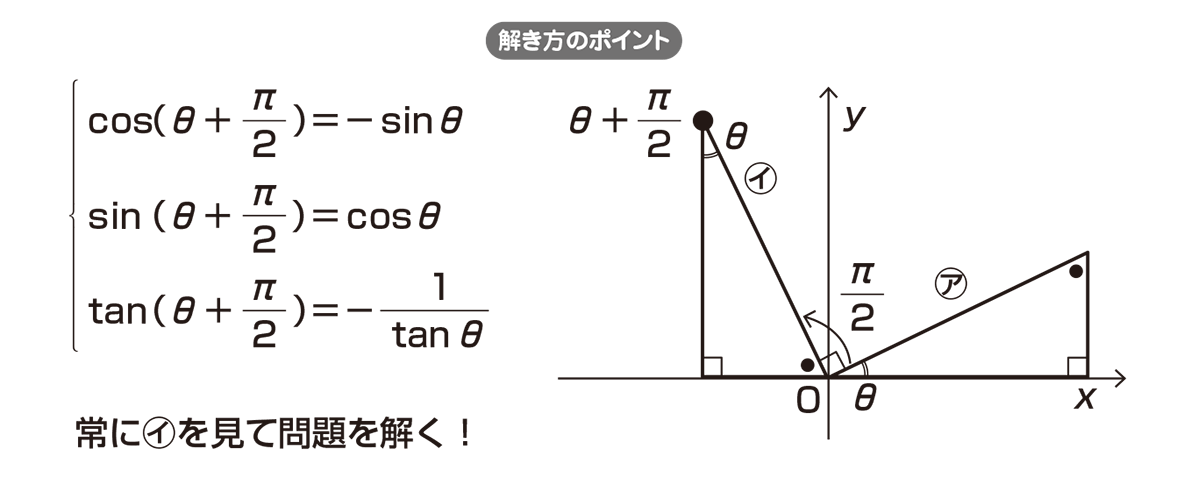
高校数学 8 と 8 P 2 の関係 映像授業のtry It トライイット

三角形の面積の三角比を用いた公式 数学の偏差値を上げて合格を目指す

3分で分かる 三角関数の基礎知識 合格サプリ

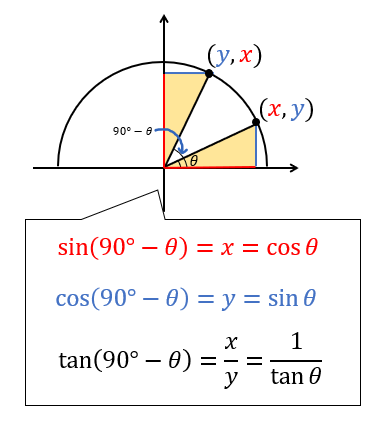
三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

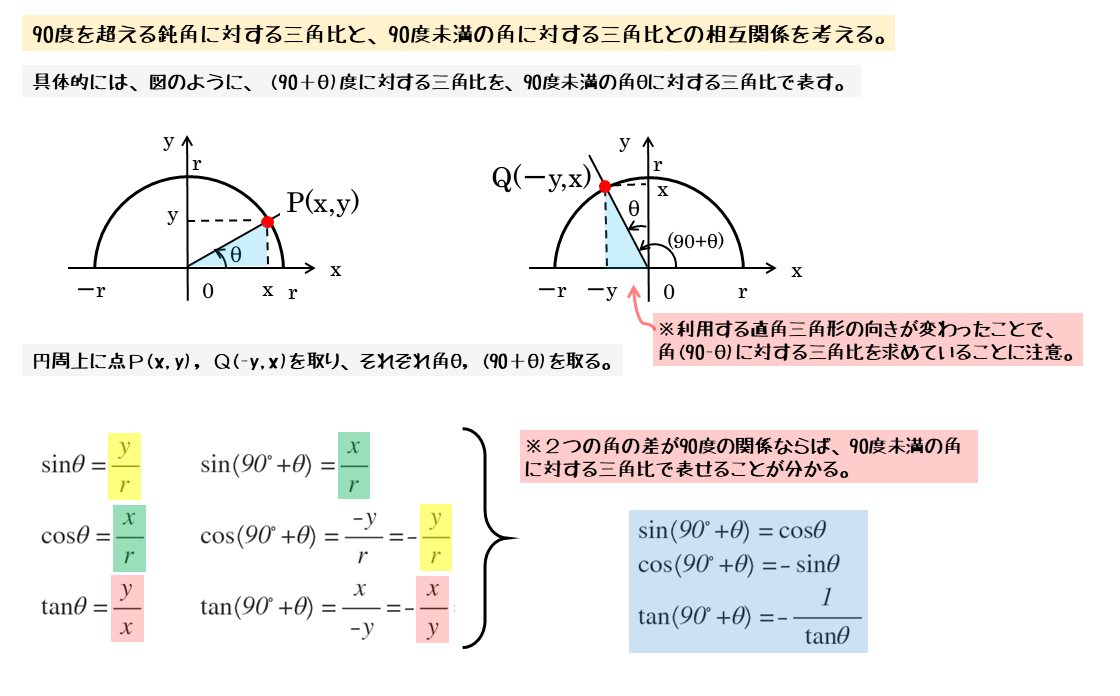
三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

逆三角関数 Wikipedia

2

基本 三角比の相互関係 なかけんの数学ノート

三角関数 逆三角関数ほか 三角関数ファミリー を紹介 空間情報クラブ 株式会社インフォマティクス

双曲線関数 おいしい数学

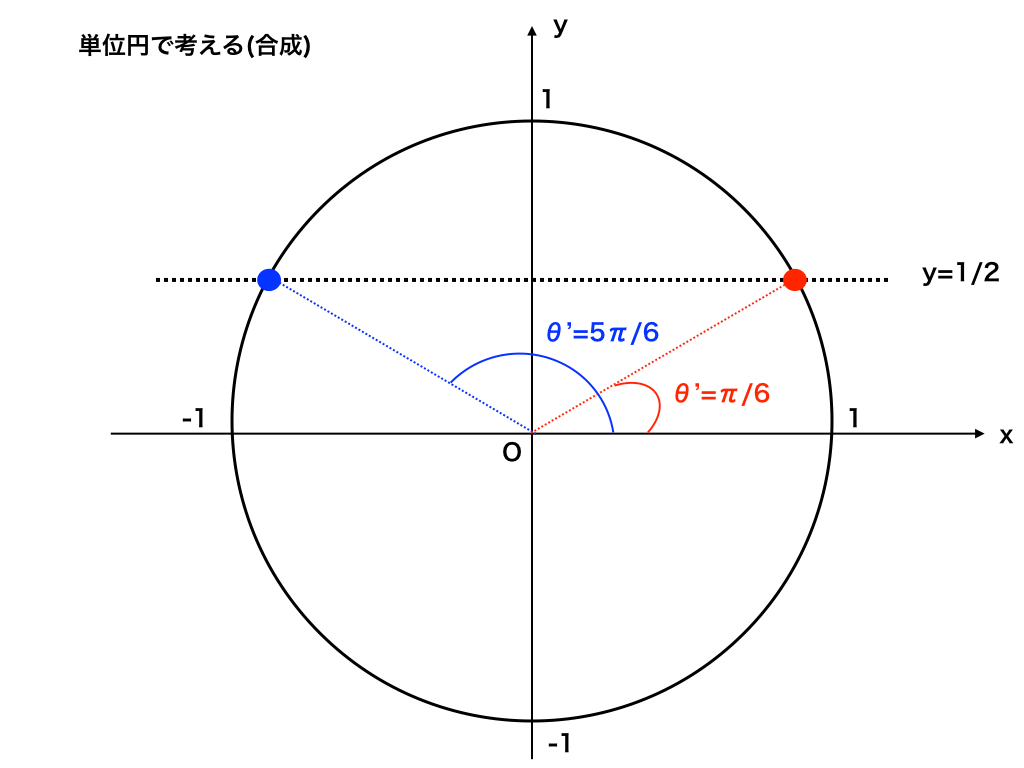
三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説

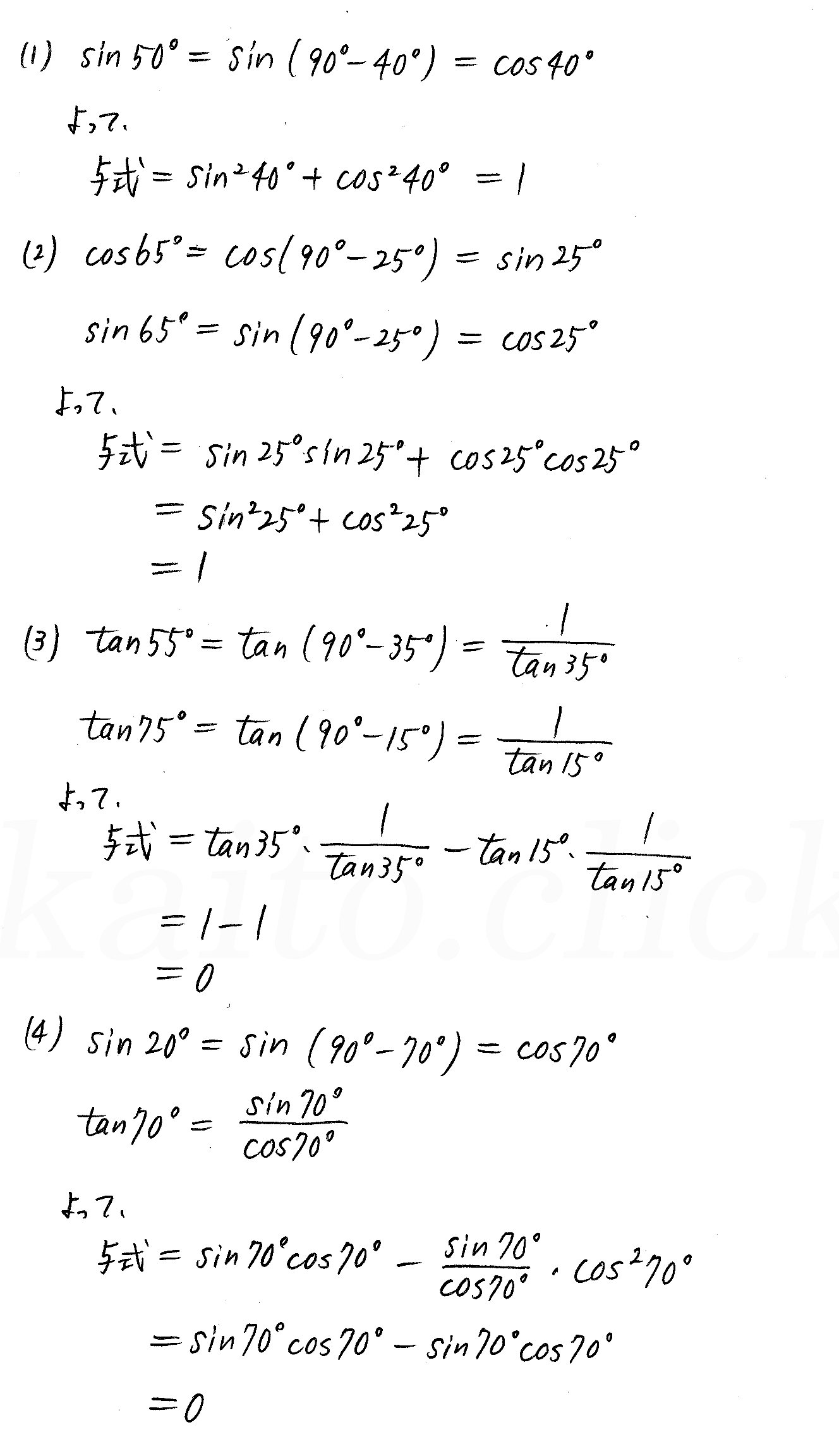
三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

三角比 三角関数を総まとめ 定義や各種公式 重要記事一覧 受験辞典

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

数学 三角関数の相互関係の公式の使い方とコツ 教科書より詳しい高校数学

基本 三角関数の相互関係 なかけんの数学ノート

三角関数 逆三角関数は何 三角関数のグラフをまとめてみました Animecreate

数学ii 三角関数 2 2 三角関数の相互関係 Youtube

Tanの値からcosの値を求めるときの分数の式変形について 数学 苦手解決q A 進研ゼミ高校講座

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

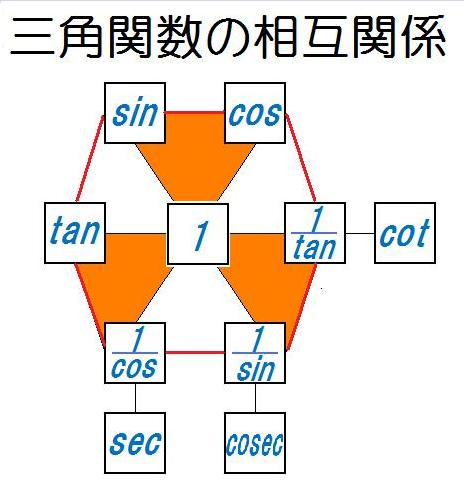
三角関数の相互関係 算数 数学記事

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

高1数学a 三角比の相互関係 なぜマイナスをつけるのかがわかりません 高校 教えて Goo

三角関数は2時間で解けるようになる 外資系コンサルタントが主夫になったら

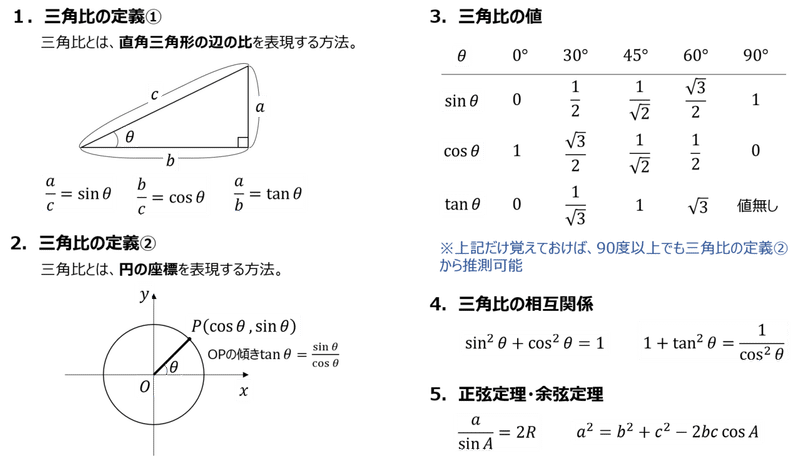
三角比は1時間で解けるようになる 箕輪 旭 Note

高校数学 三平方の定理による三角関数の計算 １ 映像授業のtry It トライイット

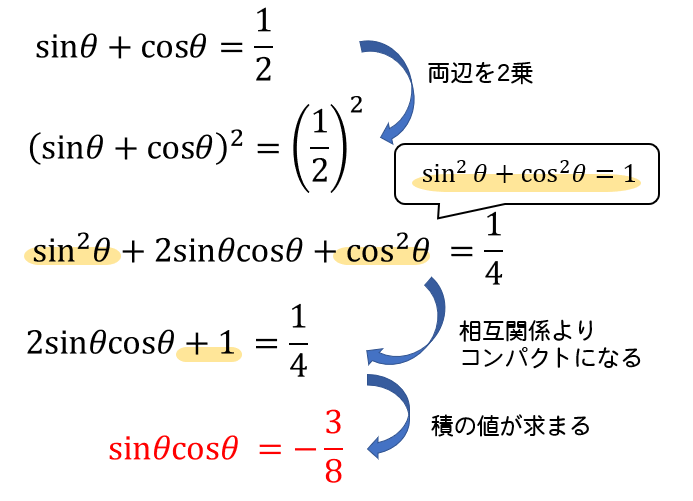
数学 三角比の式の値を求めよ 隠れた条件を見落とすな 数スタ

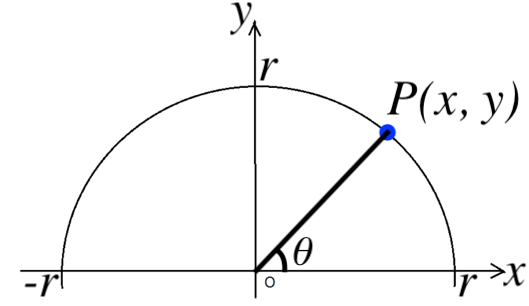
三角比を用いた計算問題をマスターしよう スタディクラブ情報局

三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説

三角関数とは コトバンク

3分で分かる 三角関数の基礎知識 合格サプリ

高校数学 三角関数の相互関係を用いる証明 例題編 映像授業のtry It トライイット

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

ここはなんでcos 8になるのですか 普通に約分できてcos8じゃないですか Clear

数2の三角関数の相互関係による式の変形の証明なんですが 2行目 Yahoo 知恵袋

1

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学

数学 三角関数 三角関数の相互関係 オンライン無料塾 ターンナップ

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

高校数学 連立三角方程式 三角関数の相互関係 合成 加法定理の利用 受験の月

3

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 Ameba News アメーバニュース

三角比の相互関係 高校数学の無料オンライン学習サイトko Su

三角関数 の基本的な定理とその有用性を再確認してみませんか その２ 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所

三角関数の相互関係 Geogebra

三角関数の相互関係 Geogebra

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

Python

三角比 三角関数 高校数学の美しい物語

三角関数の相互関係 短時間座標計算法

三角関数は2時間で解けるようになる 外資系コンサルタントが主夫になったら

三角関数の公式や簡単な計算 最大値最小値 3d Cad Cae 解析と物理の学習まで無料版simulationxpress 使い方入門編

高校数学 三角方程式 不等式 三角関数の相互関係による関数の統一 受験の月

高校数学 三角関数の相互関係を用いる証明 例題編 映像授業のtry It トライイット

数学 三角比 Sin Cos Tanの相互関係と覚え方 理系ラボ